Encyclopedia of Combinatorial Polytope Sequences...
...but it is growing. Send entry suggestions to:
Entry Editor
Searching the table:
- Ctrl-F, with sub-sequence using commas and spaces: 0, 3, 6
- or use the index of named sequences
- or
enter below any keyword or sub-sequence: vertices, facets, polygon faces or f-vectors. Use quotes: "0, 3, 6, 0" to find named entry.
Each entry of this encyclopedia is a well defined sequence P_n , array or otherwise indexed family of polytopes with a combinatorial definition. Duals (polars) to the polytopes are considered to be the same entry--just reverse the f-vectors.
Pictured are the 3d terms of polytope sequences, which have at most one term in each dimension. Pictures are often links to individual pages, which may contain more content and facilitate searching.
Below each picture is a list giving the polygon score in the 3d term: (# triangles, # squares, # pentagons, # hexagons, ...)
Immediately to the right is a list of names for the sequence: many sequences have multiple interpretations.
The sequences of numbers of vertices and facets in each dimension n begins with n=0.
The sequence labeled f-vectors is the triangle of f-vectors read by rows: each row starts with vertices, and the occurrences of 1 are the top-dimension faces.
Links are to introductory literature, not necessarily primary sources.
SEQUENCES
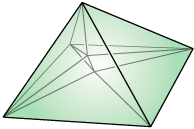
Simplex
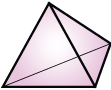
(4, 0, 0, 0)
|
Simplices Δ [wiki]
Multi-associahedron for n=2k+2 [arxiv] (V. Pilaud)
Order polytope O(P) for P the linear order on {1,...,n}. [citeseer](R.Stanley)
Chain polytope C(P) for P the linear order on {1,...,n}. [citeseer](R.Stanley)
Poset associahedra for antichain [arxiv]
Vertex cover polytope of the complete graph VC(K_n) [wiki]
edgeless-graph-associahedra [arxiv] (S. Devadoss)
(n+1)-cycle-graph graphic matroid polytopes [wiki]
Uniform matroid U^n_(n+1) polytope [wiki]
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 3, 4, 5, ... n+1 [ OEIS A000027 ]
Numbers of facets in dimension n (starting at n=0):
0, 2, 3, 4, 5, ... n+1 [ OEIS A000027 ]
f-vectors:
1, 2, 1, 3, 3, 1, 4, 6, 4, 1, 5, 10, 10, 5, 1, ... [ OEIS A135278]
|
|
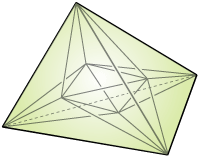
Binomial polytope B(n,n)

(4, 0, 0, 0)
|
Binomial polytopes B(n,p) with p=n [Springer] (S. Ursic)
Simplices Δ with dimension 2^n-1 [wiki]
convex_hull({truth_vector t_i | t_i is the negated truth-table row i of all {or, not} clauses using n
variables n at a time.})
Dimensions:
0, 1, 3, 7, 15 ... 2^n-1
Number of Vertices in nth polytope:
1, 2, 4, 8, 16, ... 2^n [ OEIS A000079 ]
Numbers of facets in dimension n (starting at n=0):
0, 2, 4, 8, 16, ... 2^n
[ OEIS A155559 ]
f-vectors:
1, 2, 1, 4, 6, 4, 1, 8, 28, 56, 70, 56, 28, 8, 1... [ OEIS A345135]
|
|
Demihypercube

(4, 0, 0, 0)
|
Demihypercubes; [wiki]
n-demicubes, n-hemicubes
convex_hull({alternating vertices of n-cube})
Dimensions:
1, 3, 4, ... n
Number of Vertices in nth polytope:
2, 4, 8, 16 ... 2^n [ OEIS A000079]
Numbers of facets in dimension n
2, 4, 16, 26, 44, 78,... 2^(n-1)+2n [ OEIS ?]
f-vectors:
1, 2, 1, 4, 6, 4, 1, 8, 24, 32, 16, 1, 16, 80,... [ OEIS ?]
|
|
Cut Polytope

(4, 0, 0, 0)
[polymake for n=4]
|
Cut Polytopes of complete graph CUT(n)= P_C(K_n) [Springer]
(Barahona, Mahjoub) [arXiv] (Ziegler)
[SMAPO library]
convex_hull({incidence_vector_F | F a cut of the complete graph on n nodes})
Correlation Polytopes COR(n-1) of the complete graph
[Springer] (I. Pitowski)
convex_hull({xx^T | x {0,1}-column vector of length n-1})
Binomial Polytopes B(n-1,2) [Springer] (S. Ursic)
convex_hull({truth_vector t_i | t_i is the negated truth-table row i of all {or, not} clauses using n-1 variables 2 at a time.})
|
Dimensions:
1, 3, 6, 10, 15,... (n choose 2) [ OEIS A000217]
Number of Vertices in nth polytope:
2, 4, 8, 16, 32 ... 2^(n-1) [ OEIS A000079]
Number of Facets:
2, 4, 16, 56, 368, 116764, ... OPEN [ OEIS A235459]
f-vectors:
1, 2, 1, 4, 6, 4, 1, 8, 28, 56, 68, 48, 16, 1... [ OEIS ?]
|
Flow Polytope

(4, 0, 0, 0)
[polymake for n=5,6]
|
Flow Polytopes of complete graph FLOW(n)= F(K_n) [arxiv] (Mészáros, Morales, Striker)
Chan-Robbins-Yuen Polytopes CRY(n-1)
convex_hull({incidence_vector_F | F a unit flow of the complete graph on n nodes})
Volume equals product of the first n - 2 Catalan numbers
|
Dimensions:
1, 3, 6, 10, 15,... (n-1 choose 2) [ OEIS A000217]
Number of Vertices in nth polytope:
2, 4, 8, 16, 32 ... 2^(n-2) [ OEIS A000079]
Number of Facets:
2, 4, 8, 13 ... OPEN [ OEIS ?]
f-vectors:
1, 2, 1, 4, 6, 4, 1, 8, 26, 45, 45, 26, 8, 1, 16, 98, 327, 681, 944, 897, 588, 262, 76, 13... [ OEIS ?]
|
Matching Polytope of complete graph

(4, 0, 0, 0)
[polymake for n=4]
|
Matching Polytopes of complete graph MATCH(n)= M(K_n) [wiki]
convex_hull({incidence_vector_M | M a general matching of the complete graph on n nodes}) [imsc](M. Mahajan)
|
Dimensions:
0, 1, 3, 6, 10, 15,... (n choose 2) [ OEIS A000217]
Number of Vertices in nth polytope:
1, 2, 4, 10, 26, 76, 232, 764... Sum_{k=0..[ n/2 ]} n!/((n-2*k)!*2^k*k!) [ OEIS A000085]
Number of Facets:
2, 4, 14... OPEN [ OEIS ?]
f-vectors:
1, 2, 1, 4, 6, 4, 1, 10, 39, 78, 86, 51, 14,... [ OEIS ?]
|
Fibonacci Polytope
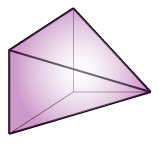
(4, 1, 0, 0)
[polymake for n=4,5]
|
Fibonacci Polytopes FP_n(2), or FP_d(k) for k=2 [
preprint ] (Fred J. Rispoli)
convex_hull({{0,1}-vector with n entries | no consecutive 1's}) (in general no k consecutive 1's)
|
Dimensions:
0, 1, 2, 3, 4, 5,... n
Number of Vertices in nth polytope:
1, 2, 3, 5, 8, 13, 21, 34... F(n) Fibonacci numbers [ OEIS A000045]
Number of Facets:
0, 2, 3, 5, 7, 9,... 2n-1 odds [ OEIS A004280]
f-vectors:
1, 2, 1, 3, 3, 1, 5, 8, 5, 1, 8, 18, 17, 7, 1, 13, 38, 48, 30, 9, 1... [ OEIS ?]
|
Hypercube
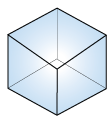
(0, 6, 0, 0)
|
Cubes C [wiki]
Order polytope O(P) for P the poset with no relations on n elements (antichain with n elements). [citeseer](R.Stanley)
Cayley polytopes C_j [arxiv](Beck, Braun, Le)
Chain polytope C(P) for P the poset with no relations on n elements (antichain with n elements). [citeseer](R.Stanley)
Lipschitz polytope L(P) for P an antichain.[Sanyal and Stump]
Lipschitz polytope L(P) for P a chain.
Stanley-Pitman polytopes Pi_n(x) [arxiv](Pitman, Stanley), [arxiv] (Postnikov, Reiner, Williams)
Acyclotopes, or graphical zonotopes, for graphs that are forests. [ Zaslavsky ], [ citeseer ], [ Postnikov ]
Voronoi cells of cographical lattice for tree graphs (primary parallelohedra, primary parallelotopes) [F. Vallentin]
Brillouin zone (Wigner-Seitz cell of reciprocal space) for Simple Cubic lattice in 3d [wiki]
Poset associahedra for cross-stack posets [arxiv]
Quotientopes P , whose upper ideal of shards contains only the basic shards.
[Pilaud, Santos]
(0,n)-Hochschild polytopes Hoch(0,n) [ arxiv ] Pilaud, Poliakova
Binomial Polytopes B(n,1) [Springer] (S. Ursic)
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 4, 8, 16, ... 2^n [ OEIS A000079 ]
Number of Facets (start at n=0):
0, 2, 4, 6, 8 ... 2*n [ OEIS A004277]
f-vectors:
1, 2, 1, 4, 4, 1, 8, 12, 6, 1, 16, ... [ OEIS A038207]
|
|
Tribonacci Polytope
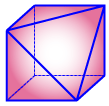
(4, 3, 0, 0)
[polymake for n=4]
|
Tribonacci Polytopes
Fibonacci Polytopes FP_n(3), or FP_d(k) for k=3 [
preprint ] (Fred J. Rispoli)
convex_hull({{0,1}-vector with n entries | no 3 consecutive 1's}) (in general no k consecutive 1's)
|
Dimensions:
0, 1, 2, 3, 4, 5,... n
Number of Vertices in nth polytope:
1, 2, 4, 7, 13, 24... Trib(n) Tribonacci numbers [ OEIS A000073]
Number of Facets:
0, 2, 4, 7, 10, 13,... 3n-2 [ OEIS A033627]
f-vectors:
1, 2, 1, 4, 4, 1, 7, 12, 7, 1, 13, 31, 28, 10, 1... [ OEIS ?]
|
Independent set polytope of Uniform matroid

(4, 3, 0, 0)
|
Uniform matroid U^(n-1)_n independent set polytope [arxiv] (Ardila, Benedetti, Doker)
n-cycle-graph graphic matroid independent set polytopes [wiki]
Dimensions:
1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 3, 7, 15, ... 2^n - 1 [ OEIS A000225]
Number of Facets (start at n=0):
0, 0, 3, 7, ...
|
|
Bipartite Subgraph Polytope

(4, 3, 0, 0)
|
Bipartite Subgraph Polytopes of the complete graph P_B(K_n) = BS(n)
[jstor](F. Barahona, M. Grötschel, A. Mahjoub)
[SMAPO library(large subgraphs only)]
|
Dimensions:
0, 1, 3, 6, 10 ... (n choose 2)
Number of Vertices in nth polytope:
1, 2, 7, 41, 376, ... [ OEIS A047864]
Number of Facets (start at n=1):
0, 2, 7, ...
|
Tutte Polytope
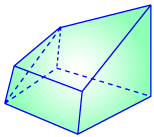
(2, 5, 0, 0)
[polymake for 3D]
|
Tutte Polytopes T_i [arxiv]
(Konvalinka, Pak)
Volumes equal evaluated Tutte polynomials of complete graphs.
|
Dimensions:
1, 2, 3, 4, ... n
Number of Vertices in nth polytope:
2, 4, 8, 16, 32, ... 2^n [ OEIS A000079]
Number of Facets:
2, 4, 7, 11, 16, 22, 29, ... (n+1)n/2 + 1 [ OEIS A000124]
f-vectors:
1, 2, 1, 4, 4, 1, 8, 13, 7, 1, 16, 37, 32, 11, 1, ... [ OEIS ?]
|
Cubeahedron (edgeless graph)
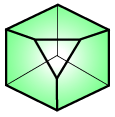
(1, 3, 3, 0)
|
Edgeless-graph cubeahedra [arxiv] (Devadoss, Heath, Vipismakul)
Range quotient of edgeless-graph multiplihedron JGr
[arxiv] (Devadoss, Forcey) |
Dimensions:
1, 2, 3, ... n
Number of Vertices in nth polytope:
2, 5, 10, ... 2^n + n-1 [ OEIS A052944 ]
Number of Facets (start at n=0):
0, 2, 5, 7, 9, ... 2*n + 1 [ OEIS A130773 ]
|
Linear Ordering Polytope
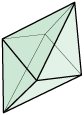
(8, 0, 0, 0)
|
Linear ordering polytopes P_LO [zib.de] (M. Grötschel, M. Jünger, G. Reinelt),
[citeseer] (T. Christof, G. Reinelt),
[arxiv] (Katthän), [SMAPO library]
Binary choice polytopes
convex_hull({char_vector_LO | LO a linear order with n elements})
|
Dimensions:
0, 1, 3, 6, 10, ... (n choose 2)
Number of Vertices in nth polytope:
1, 2, 6, 24, ... n! [ OEIS A000142][see: i, ii, iii]
Number of Facets:
0, 2, 8, 20, 40, 910, 87472 ... OPEN [ OEIS ?]
f-vectors:
1, 2, 1, 6, 12, 8, 1, 24, ... [ OEIS ?]
|
Acyclotope (Tadpole graph)
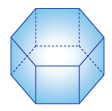
(0, 6, 0, 2)
|
Quotientopes P , whose upper ideal of shards contains the basic shards,
and (1, 3, {2}), and (1, 3, {}).
[Pilaud, Santos]
Acyclotopes A(T_3,n) for tadpole graphs T_3,n, with n+3 nodes.
[ Zaslavsky ], [citeseer]
Graphical zonotopes for tadpole graphs Z(T_3,n)
[Postnikov]
Voronoi cells of cographical lattice for tadpole graphs T_3,n (primary parallelohedra, primary parallelotopes) [F. Vallentin]
Dimensions:
0, 1, 2, 3, ... n+2
Number of Vertices in nth polytope:
1, 2, 6, 12, 24, 48, ... 6*2^n acyclic orientations of the tadpole graph on n+3 nodes[ OEIS A007283]
Number of Facets:
0, 2, 6, 10, 14, ... 6+2n directed edge cuts of the tadpole graph on n+3 nodes [ OEIS A005843]
|
|
Freehedron
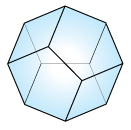
(0, 4, 4, 0)
|
Freehedra F [arxiv] (Saneblidze)
(1,n)-Hochschild polytopes Hoch(1,n) [ arxiv ] Pilaud, Poliakova
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
2, 5, 12, 28, 64, 144, 320, 704...(n+3)*2^(n-2) [Conj. OEIS A045623] (F. Chapoton)
Number of Facets:
0, 2, 5, 8, 11 ... 3*n - 1 [ OEIS A016789]
|
|
Associahedron
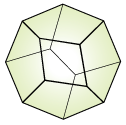
( 0, 3, 6, 0)
|
Associahedra K, Y [claymath] (J.L. Loday)
Stasheff polytopes, Tamari-Stasheff polytopes [book chapter] (J. Stasheff)
Type A associahedra [arxiv] (Fomin, Reading)
Amplituhedron for biadjoint scalar phi^3 theory [arxiv](Arkani-Hamed, Bai, He,Yan)
Secondary polytope of the set of vertices of a polygon [maa review] (Gelfand, Kapranov, Zelevinsky)
Newton polytope of the discriminant polynomial of the (integer coordinate) vertices of a polygon.
Multi-associahedron Delta(n,1) for k=1. [arxiv] (Pilaud, Santos)
Fiber polytope of the simplex over a polygon. [jstor] (Billera, Sturmfels)
Path graph associahedra [arxiv] (Carr, Devadoss)
Path graph cubeahedra [arxiv] (Devadoss, Heath, Vipismakul)
Zig-zag poset associahedra [arxiv] (Devadoss et.al.)
Chain (Galashin) poset associahedra [arxiv] (P. Galashin)
Path graph operahedra [arxiv] (G. Laplante-Anfossi)
Quotientopes P , whose upper ideal of shards contains the basic shards and all upper shards.
[Pilaud, Santos]
2-associahedra W_n for the sequence(n). [arxiv](N. Bottman)
(1,n) biassociahedra KK(n,1), KK(1,n) [arxiv] (Saneblidze, Umble)
alt. notation B^n_1, B^1_n [arxiv] (Markl)
Constrainahedra C(1,n) = C(n,1),
[ arxiv ] ( Bottman, Poliakova)
or Constr(0,n) = Constr(n,0), [ arxiv ] ( Chapoton, Pilaud)
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 5, 14, 42, ... Catalan numbers [ OEIS A000108]
Number of Facets:
0, 2, 5, 9, 14, ... Triangular numbers minus one [ OEIS A000096 ]
f-vectors:
1, 2, 1, 5, 5, 1, 14, 21, 9, 1, 42, 84, 56, 14, 1, ... [ OEIS A033282]
h-vectors:
1, 3, 1, 1, 6, 6, 1, 1, 10, 20, 10, 1, 1, 15, 50, 50, 15, 1... [ OEIS A001263]
|
|
Type D Associahedron

( 0, 3, 6, 0)
|
Type D associahedra [arxiv] (Fomin, Reading) [arxiv] (Ceballos, Pilaud)
Dimensions:
2, 3, ... n
Number of Vertices in nth polytope:
4, 14, 50, 182 ... (3n-2)*C(n-1), where C is Catalan numbers [ OEIS A051924]
Number of Facets:
4, 9, 16, 25 ... n^2 [ OEIS A000290]
f-vectors:
1, 4, 4, 1, 14, 21, 9, 1, 50, 100, 66, 16, 1, ... [ OEIS A080721]
|
|
Multipath (pseudograph) associahedron
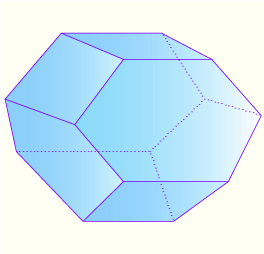
(0, 5, 2, 2)
|
2-path associahedra P(n,2); P(n,1) , for the multipath formed by doubling all edges
of the path on n nodes, or respectively all but the last edge.
[arxiv] Carr, Devadoss, Forcey
2-associahedra W_1, W_10, W_101, W_1010, ... .
[arxiv](N. Bottman)
Poset associahedra for the poset of the 2-paths.
[arxiv] (Devadoss et.al.)
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 4, 14, ... ? [ OEIS ?]
Number of Facets:
0, 2, 4, 9, ... ? [ OEIS ?]
f-vectors:
1, 2, 1, 4, 4, 1, 14, 21, 9, 1, ... [ OEIS ?]
|
|
Composihedron
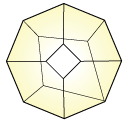
(0, 4, 6, 0)
|
Composihedra CK [arxiv] (Forcey)
Path-graph composihedra [arxiv] (Devadoss, Forcey)
(in low dimensions) pasting diagrams of pseudomonoids in monoidal 2-categories [TAC] (P. McCrudden)
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 5, 15, 51, ... binomial transform of Catalan numbers [ OEIS A007317]
Number of Facets:
0, 2, 5, 10, 19 ... 2^n+n-1 [ OEIS A052944]
|
Halohedron
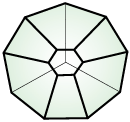
(0, 3, 6, 1)
|
Halohedra H [arxiv] (Devadoss, Heath, Vipismakul)
Cycle-cubeahedra
[arxiv] (Devadoss, Forcey)
1-loop Amplituhedron for planar ϕ^3 theory
[arxiv] (Salvatori)
|
Dimensions:
1, 2, 3, ... n
Number of Vertices in nth polytope:
2, 5, 16, 55, 196, ... Catalan(n)*(3n+2)[ OEIS A051960]
Number of Facets:
0, 2, 5, 10, 17, ... n^2+1 [ OEIS A002522]
|
Graph composihedron (cycle graph)

(0, 3, 6, 1)**
|
Cycle-composihedra JGd
[arxiv] (Devadoss, Forcey)
Dimensions:
1, 2, 3, ... n
Number of Vertices in nth polytope:
2, 5, 16, 61 ... OPEN [ OEIS ?]
Number of Facets:
0, 2, 5, 10, ... OPEN [ OEIS ?]
|
|
Stellohedron

(0, 3, 6, 1)
|
Stellohedra S [arxiv] (Postnikov, Reiner, Williams)
Secondary polytopes of pairs of nested concentric n-dimensional simplices. [arxiv] (V. Pilaud, T. Manneville)
Star-graph associahedra [arxiv] (Carr, Devadoss)
complete-graph-cubeahedra [arxiv] (Devadoss, Heath, Vipismakul)
complete-graph-composihedra JGd [arxiv] (Devadoss, Forcey)
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 5, 16, 65, ... Sum_{k=0..n} n!/k! [ OEIS A000522][see: i]
Number of Facets:
0, 2, 5, 10, 19, 36, ... 2^n + n - 1 [ OEIS A052944 ] (Thanks to P. Showers)
f-vectors:
1, 2, 1, 5, 5, 1, 16, 24, 10, 1, 65, 130, ... [ OEIS A248727] (Thanks to Tom Copeland)
h-vectors:
1, 3, 1, 1, 7, 7, 1, 1, 15, 33, 15, 1, 1, 31, 131, 131, 31, 1, ...[ OEIS A046802] (Thanks to Tom Copeland)
|
|
Graph composihedron (edgeless graph)
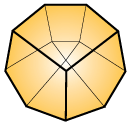
(1, 6, 3, 0)
|
Edgeless-graph-composihedra JGd
[arxiv] (Devadoss, Forcey)
Dimensions:
1, 2, 3, ... n
Number of Vertices in nth polytope:
2, 5, 13, ... OPEN [ OEIS ?]
Number of Facets:
0, 2, 5, 10, ... OPEN [ OEIS ?]
|
|
Graph multiplihedron (edgeless graph)
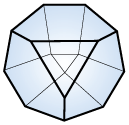
(2, 6, 0, 3)
|
Edgeless-graph-multiplihedra JG
[arxiv] (Devadoss, Forcey)
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 15, 36, ... n*2^(n-1) + n [ OEIS A215149]
Number of Facets:
0, 2, 6, 11, 20, ... 2^n + n [ OEIS ?]
|
|
Cyclohedron
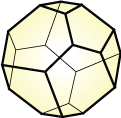
(0, 4, 4, 4)
|
Cyclohedra W
[arxiv] (M. Markl)
Bott-Taubes polytopes
Type B,C associahedra
[arxiv] (S. Fomin, N. Reading)(R. Simion)
cycle-graph-associahedra [arxiv] (S. Devadoss)
(in low dimensions) hexagonator equations (pasting diagrams) in braided monoidal categories [arxiv] (M. Stay)
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 20, 70, ... central binomial coefficients [ OEIS A000984]
Number of Facets:
0, 2, 6, 12, 20, ... n^2+n [ OEIS A002378]
f-vectors:
1, 2, 1, 6, 6, 1, 12, 30, 20, 1, 20, 90, 140, ... [ OEIS A063007]
|
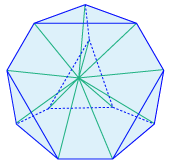
Acyclotope (cycle graph)
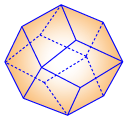
(0, 12, 0, 0)
|
Acyclotopes for cycle graph A(G)
[ Zaslavsky ], [ citeseer ]
Graphical zonotopes for cycle graph Z(G)
[Postnikov]
Voronoi cells of cographical lattice for cycle graphs (primary parallelohedra, primary parallelotopes) [F. Vallentin]
Brillouin zone (Wigner-Seitz cell of reciprocal space) for Body Centered Cubic lattice in 3d [wiki]
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 14, 30, ... acyclic orientations of (n+1)-cycle = 2^(n+1) - 2 [ OEIS A000918]
Number of Facets:
0, 2, 6, 12, 20, ... directed edge cuts of the (n+1)-cycle = n^2+n [ OEIS A002378]
|
|
Acyclotope (zigzag ladder graph)
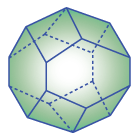
(0, 8, 0, 4)
|
Quotientopes P , whose upper ideal of shards contains the basic shards, and (i, i+2, {i+1}), and (i, i+2, {}).
[Pilaud, Santos]
Acyclotopes A(G) for zigzag ladder graph G, with n+1 nodes, and edges { i,i+1}, and {i,i+2}.
[ Zaslavsky ], [citeseer]
Graphical zonotopes for zigzag ladder graph Z(G)
[Postnikov]
Voronoi cells of cographical lattice for zigzag ladder graphs (primary parallelohedra, primary parallelotopes) [F. Vallentin]
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 18, 54, 162, ... 2*3^n acyclic orientations of zigzag ladder [ OEIS A008776 ]
Number of Facets:
0, 2, 6, 12, 20, ... n^2+n directed edge cuts of the zigzag ladder on n+1 nodes [ OEIS A002378]
|
|
Acyclotope (fan graph)

(0, 8, 0, 4)
|
Acyclotopes A(F_1,n) for fan graphs F_1,n.
[ Zaslavsky ], [citeseer]
Graphical zonotopes for fan graph Z(F_1,n)
[Postnikov]
Shuffle polytope of Path graph and Point graphical zonotopes. [ arxiv ] (Chapoton, Pilaud)
Voronoi cells of cographical lattice for fan graphs (primary parallelohedra, primary parallelotopes) [F. Vallentin]
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 18, 54, 162, ... 2*3^n acyclic orientations of fan graph
[ OEIS A025192 ]
Number of Facets:
0, 2, 6, 12, 20, ... n^2+n directed edge cuts of the fan graph on n+1 nodes [ OEIS A002378]
|
|
Multiplihedron
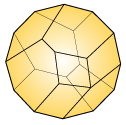
(0, 6, 2, 5)
|
Multiplihedra J, M
[arxiv] (Forcey)
Path-graph-multiplihedra JP_n
[arxiv] (Devadoss, Forcey)
2-associahedra W_n0 = W_0n for the sequences(n,0) or (0,n). [arxiv](N. Bottman)
Step 1 Biassociahedra K^2_n
[arxiv](M. Markl)
(in low dimensions) trihomomorphism axioms (pasting diagrams) in tricategories [books] (Gordon, Power, Street)
Constrainahedra C(2,n) = C(n,2),
[ arxiv ] ( Bottman, Poliakova)
or Constr(1,n) = Constr(n,1), [ arxiv ] (Chapoton, Pilaud)
(1,n)-Multiplihedra Mult(1,n) [ arxiv ] Pilaud, Poliakova
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 21, 80, ... Catalan transform of Catalan numbers [ OEIS A121988]
Number of Facets:
0, 2, 6, 13, 25, 46, ... n(n + 1)/2+ 2^n - 1. [ OEIS ?][see: i]
|
Path-graph Tubing polytope
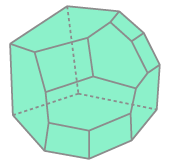
(0, 6, 0, 7)
|
Path-graph Tubing polytope T
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 22, 90, ... Large Schröder numbers [ OEIS A006318]
Number of Facets:
0, 2, 6, 13, ... [ OEIS ?][see: i]
|
(2,n)-Brick Polytope
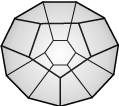
(0, 5, 2, 6)**
|
(2,n)-Brick Polytopes B^2(n)
[arxiv](V. Pilaud)
convex hulls of the brick vectors of all (2, n)-twists
Brick Polytopes of the 2-kernels of
(size n) bubble sort networks Omega(B^2_(n+4))
[arxiv](V. Pilaud, F. Santos)
• (2,n)-Beam Polytopes Omega_(2,n) [arxiv](V. Pilaud)
|
Dimensions:
0, 1, 2, 3, ... n-1
Number of Vertices in nth polytope:
1, 2, 6, 22, 92, 420, 2042, ... [ OEIS A263791] and
[ OEIS conjecture A264868]
Number of Facets:
0, 2, 6, 13, 25, 45, 78, 132, ... [ OEIS A065220]
f-vectors:
1, 2, 1, 6, 6, 1, 22, 33, 13,
1, 92, 185, 118, 25, 1, 420, 1062, 945, 346, 45, ... [ OEIS ?]
|
Pterahedron

(0, 5, 2, 6)
|
Pterahedra P_t
[L. Berry]
fan-graph-associahedra [arxiv] (S. Devadoss)
|
Dimensions:
0, 1, 2, 3, ... n-1
Number of Vertices in nth polytope:
1, 2, 6, 22, 94, 464, ... Catalan transform of the factorials [ OEIS ?]
Number of Facets:
0, 2, 6, 13, 25, 46, ... n(n + 1)/2+ 2^n - 1. [ OEIS ?][see: i]
f-vectors:
1, 2, 1, 6, 6, 1, 22, 33, 13, 1, 94, ... [ OEIS ?]
|
Permutohedron, permutahedron
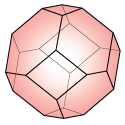
(0, 6, 0, 8)
|
(Type A) Permutohedra/ permutahedra P, S
[wiki]
Secondary polytopes of the prisms of simplices. [e-book] (Gelfand, Kapranov, Zelevinsky)
complete-graph-associahedra [arxiv] (S. Devadoss)
complete-graph-multiplihedra [arxiv] (Devadoss, Forcey)
Path graph graphicahedra [arxiv] (Schulte et al.)
Star-graph operahedra (since the line graph of a star graph is complete) [arxiv] (Ward) [arxiv] (Laplante-Anfossi)
Step 1 Bipermutohedra P^n_m
[arxiv](M. Markl)[arxiv](S.Saneblidze, R. Umble)
Step 1 Biassociahedra K(n,m) = K^n_m
[arxiv](M. Markl)[arxiv](S.Saneblidze, R. Umble)
Acyclotopes for complete graphs A(K_n)
[ Zaslavsky ], [ citeseer ]
Graphical zonotopes for complete graphs Z(K_n)
[Postnikov]
Zonotopes polar to the braid arrangements.
Fiber polytopes of unit cubes over line segments. [jstor] (Billera, Sturmfels)
Voronoi cells of cographical lattice for complete graphs (primary parallelohedra, primary parallelotopes) [F. Vallentin]
Brillouin zone (Wigner-Seitz cell of reciprocal space) for Face Centered Cubic lattice in 3d [wiki]
Poset-associahedra for antichain with minimal element adjoined (claw) [arxiv](Devadoss et.al.)
(Galashin) poset associahedra for antichain with minimal element adjoined (claw) [arxiv] (P. Galashin)
Quotientopes P , whose upper ideal of shards contains all the shards.
[Pilaud, Santos]
1-skeleton is Cayley graph for symmetric group, using transpositions.[wiki]
Edgeless graph-Cosmohedra [arxiv] (R. Glew, T. Lukowski)
Single (universal) edge hypergraph Acyclonesto-cosmohedra [arxiv] (S. Forcey, R. Glew, H. Kim)
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 24, 120, ... n! [ OEIS A000142][see: i, ii, iii]
Number of Facets:
0, 2, 6, 14, 30 ... 2^(n+1) -2 [ OEIS A000918]
f-vectors:
1, 2, 1, 6, 6, 1, 24, 36, 14, 1, ... [ OEIS A019538]
h-vectors:
1, 4, 1, 1, 11, 11, 1, 1, 26, 66, 26, 1, ... [ OEIS A008292]
|
Type D permutohedron

(0, 6, 0, 8)
|
Type D permutohedra PD
[zib.de] (Reiner, Ziegler)
Dimensions:
2, 3, ... n
Number of Vertices in nth polytope:
4, 24, 192, ... 2^(n-1)*n! [ OEIS A002866]
Number of Facets:
4, 14, 48, ... 3^n - n*2^(n-1) - 1 [ OEIS ?] (Thanks N. Reading)
f-vectors:
1, 4, 4, 1, 24, 36, 14, 1, 192, 384, 240, 48, 1,... [ OEIS A145902]
|
|
Graph multiplihedron (cycle graph)

(0, 6, 0, 8)**
[polymake for n=4]
|
Cycle-multiplihedra JG
[arxiv] (Devadoss, Forcey)
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 24, 104, ... OPEN [ OEIS ?]
Number of Facets:
0, 2, 6, 14, 28, ... OPEN [ OEIS ?]
f-vectors:
1, 2, 1, 6, 6, 1, 24, 36, 14, 1, 104, 210, 134, 28... [ OEIS ?]
|
(3,n) Brick Polytope

(0, 6, 0, 8)**
|
(3,n)-Brick Polytopes B^3(n)
[arxiv](V. Pilaud)
convex hulls of the brick vectors of all (3, n)-twists
Brick Polytopes of the 3-kernels of
(size n) bubble sort networks Omega(B^3_n)
[arxiv](V. Pilaud, F. Santos)
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 24, 114, 612, 3600, ... [ OEIS A263791] and
[ OEIS ?]
Number of Facets:
0, 2, 6, 14, 29, 57, 109, 205, ... OPEN [ OEIS ?]
|
2-associahedron for sequence (0,n,0)

(0, 6, 0, 8) conj. polytope
|
(0,n,0) 2-associahedra W_0n0
[arxiv](N. Bottman)
Faces are 2-tubings based on the sequence 0,n,0
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 24, 108, 520, 2620, 13648, 72956, ... OPEN [ OEIS ?]
Number of Facets:
0, 2, 6, 14, 29, 57, 110, 212, ... OPEN [ OEIS ?]
|
Strong Rectangulotopes

(0, 6, 0, 8)
|
Strong Rectangulotopes SR(n)
[ Cardinal, Pilaud]
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 6, 24, 116, 642, 3938, 26194, ...OPEN [ OEIS ]
Number of Facets:
0, 2, 6, 14, 30, 62 ... 2^(n+1)-2 [ OEIS ?]
|
Diagonal rectangulation polytope
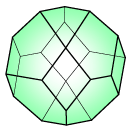
(0, 6, 4, 4)
|
Diagonal rectangulation polytopes
[arxiv] (Law, Reading)
Quotientopes P , whose upper ideal of shards contains the basic shards, all upper shards, and all lower shards.
[Pilaud, Santos]
Weak Rectangulotopes WR(n) [ Cardinal, Pilaud]
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope: 1, 2, 6, 22, 92, ... Baxter permutations [ OEIS A001181]
Number of Facets:
0, 2, 6, 14, 30 ... 2^(n+1) -2 [ OEIS A000918]
|
Ordered partial partition polytope
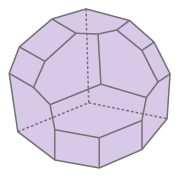
(0, 6, 0, 9)
|
Ordered partial partition polytope (Determinant volume polytopes) F_A
[arxiv] (R. Houston, A. Goucher, N. Johnston)
Complete Graph Tubing polytopes,
[A. Goucher]
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope: 1, 2, 6, 26, 150, 1082, ... , Sum_{k>=1} k^n/2^k. [ OEIS A000629]
Number of Facets:
0, 2, 6, 15, 36, 85, 198, ... n * (1 + 2^(n-1)) [ OEIS A215149]
f-vectors:
1,
2, 1,
6, 6, 1,
26, 39, 15, 1,
150, 300, 186, 36, 1, ...
|
Cycle graph tubing polytope

(0, 6, 0, 9)
|
Cycle Graph Tubing polytopes,
[A. Goucher]
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope: 1, 2, 6, 26, 126, 642, ... [ OEIS ? ]
Number of Facets:
0, 2, 6, 15, [ OEIS ? ]
f-vectors:
1,
2, 1,
6, 6, 1,
26, 39, 15, 1,
126, ...
|
Type B permutohedron
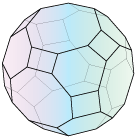
(0, 12, 0, 8, 0, 6)
Image redrawn from Fig. 2.4 of [Fomin, Reading] |
Type B permutohedra PB
[arxiv] [Fomin, Reading]
Conjectured: Acyclotopes of signed complete graphs [Zaslavsky]
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 8, 48, 384, ... 2^n*n! = (2n)!! [ OEIS A000165][see: i]
Number of Facets:
0, 2, 8, 26, 80, ... 3^n-1 [ OEIS A024023] (Thanks to N. Reading)
f-vectors:
1, 2, 1, 8, 8, 1, 48, 72, 26, 1, ... [ OEIS A145901 (dual)]
|
Cosmohedra
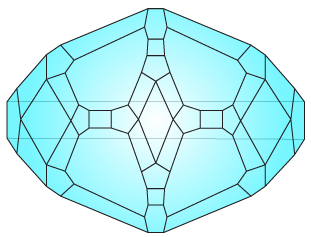
(0, 24, 12, 2, 0, 0, 0, 6)
|
Cosmohedra P
[arxiv] [Nima Arkani-Hamed, Carolina Figueiredo, Francisco Vazão]
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 10, 72, 644, 6704...
Number of Facets:
0, 2, 10, 44, 196, 902... (1/(n-1))*Sum_{k=0..n-3} binomial(n-1,k+1)*binomial(n-3,k)*2^(n-3-k) -1 [ OEIS A001003 -1]
f-vectors:
1, 2, 1, 10, 10, 1, 72, 114, 44, 1, 644, 1400, 952, 196, 1... [ OEIS ? ]
|
Type B Coxeter-associahedron
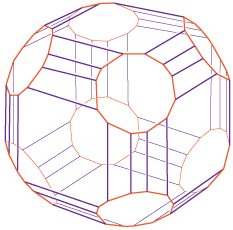
(0, 36, 0, 0, 0, 6, 0, 0, 0, 8)
Image redrawn from Fig. 3 of [Reiner, Ziegler],
original credited to Jürgen Richter-Gebert.
|
Type B Coxeter-associahedra KPB
[zib.de] [Reiner, Ziegler]
|
Dimensions:
1, 2, 3, ... n
Number of Vertices in nth polytope:
2, 8, 96, ... 2^n*n!*(Catalan number) [ OEIS conjecture]
Number of Facets:
2, 8, 50, ... OPEN [ OEIS ?]
|
Type A Coxeter-associahedron (Permutoassociahedron)
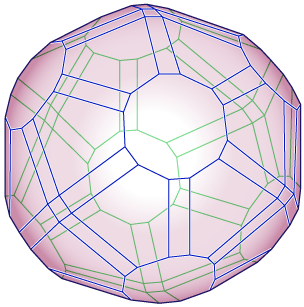
(0, 42, 24, 0, 0, 0, 0, 0, 0, 8)
Image redrawn from Fig. 4 of [Reiner, Ziegler],
original credited to Jürgen Richter-Gebert.
|
Type A Coxeter-associahedra KPA
[zib.de] (Reiner, Ziegler_
Permutoassociahedra, Permuto-associahedra KP
[M. Batanin, via R. Street]
Complete graph-Cosmohedra [arxiv] (R. Glew, T. Lukowski)
Claw-poset acyclonesto-cosmohedra [arxiv] (S. Forcey, R. Glew, H. Kim)
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 12, 120, 1680... n!*(Catalan number) [ OEIS ]
Number of Facets:
0, 2, 12, 74, ... Ordered Bell numbers -1 [ OEIS A000670][ OEIS A052875]
f-vectors:
1, 2, 1, 12, 12, 1, 120, 192, 74, 1, ...
[ OEIS ?]
|
|
Type D Coxeter-associahedra
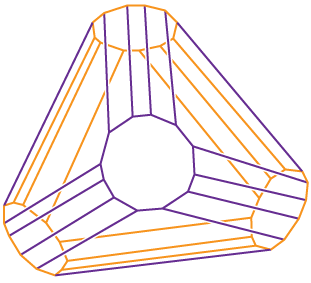
(0, 18, 0, 4, 0, 0, 0, 0, 0, 4)
Image redrawn from Fig. 3 of [Reiner, Ziegler],
original credited to Jürgen Richter-Gebert.
|
Type D Coxeter-associahedra KPD
[zib.de] [Reiner, Ziegler]
|
Dimensions:
0, 1, 2, 3, ... n
Number of Vertices in nth polytope:
1, 2, 4, 48, ... [ OEIS ? ]
Number of Facets:
0, 2, 4, 26, ... [ OEIS ?]
f-vectors:
1, 2, 1, 4, 4, 1, 48, 72, 26, 1, ...
|
(Polars of) Even Dimensional Cyclic Polytopes with d+3 vertices
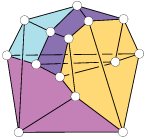
(No 3d term)
|
(Polars of) C(2k+3,2k) Alternating Cyclic Polytopes [ wiki]
Multiassociahedra: k-triangulations of the (2k+3)-gon
[ arxiv ] ( V. Pilaud )
(Polars of) Amplituhedra A(d+3,1,d)
the alternating polytopes of dimension d with d+3
vertices (in projective space)[ arxiv ]
( S. Karp, L. Williams)
|
Dimensions:
2, 4, 6, 8,... 2k
Number of Vertices in kth polytope:
5, 14, 30, 55, 91, 140, 204 ... ((k+3) choose 3)+((k+2) choose 3) [OEIS A000330 ]
Number of Facets:
5, 7, 9, 11... 2k+3
f-vectors:
1, 5, 5, 1, 14, 28, 21, 7, 1, 30, 90, 117, 84, 36, 9, 1, 55, 220, 407, 451, 330, 165, 55, 11, 1...
|
Symmetric Path Polytope
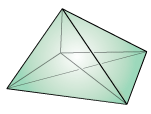
(No 3d term)
[polymake for n=4,5]
|
s-t Path Polytopes of complete graph Path(n)= Path(K_n), n>1 [Springer] (A. Schrijver)
convex_hull({incidence_vector_F | F a path from node s to node t of the complete graph on n nodes})
|
Dimensions:
0, 1, 4, 8,... conject. (n choose 2)-2 [ OEIS A034856]
Number of Vertices in nth polytope:
1, 2, 5, 16, 65, ... Sum_{k=0..(n-2)} (n-2)!/k! [ OEIS A000522][see: i]
Number of Facets:
2, 5, 25, ... OPEN [ OEIS ?]
f-vectors:
1, 2, 1, 5, 10, 10, 5, 1, 16, 102, 334, 622, 685, 442, 156, 25, 1... [ OEIS ?]
|
Birkhoff polytope
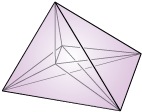
(No 3d term.)
[polymake for n=3]
[
Sage library]
|
Birkhoff polytopes B [wiki]
assignment polytope
Transportation polytope Trans_n(1, 1, . . . , 1) [arxiv] (Mészáros, Morales, Rhoades)
perfect matching polytope of complete bipartite graph
set of doubly stochastic matrices
convex_hull({M | M an nxn permutation matrix})
Dimensions:
0, 1, 4, 9, 16 ... (n-1)^2
Number of Vertices in nth polytope:
1, 2, 6, 24, ... n! [ OEIS A000142][see: i, ii, iii]
Number of Facets:
0, 2, 9, 16,... n^2 [ OEIS A000290]
f-vectors:
1, 2, 1, 6, 15, 18, 9, 1 ... [ OEIS ?]
|
|
Alternating Sign Matrix Polytope
(No 3d term.)
[polymake for n=3]
|
Alternating Sign Matrix polytopes ASM(n) [arXiv] (J. Striker)
convex_hull({char_vector_ASM | ASM an nxn alternating sign matrix })
|
Dimensions:
0, 1, 4, 9, 16, ... (n-1)^2
Number of Vertices in nth polytope:
1, 2, 7, 42, 429, 7436,... Product[j=0..n-1](3j+1)!/(n+j)! [ OEIS A005130]
Number of Facets:
0, 2, 4, 8, 20, 40, 68, 104,...,4[(n-2)^2 +1][ OEIS A128445]
f-vectors:
1, 2, 1, 7, 17, 18, 8, 1, 42, ... [ OEIS ?]
|
Linear signed order polytope
(No 3d term)
[polymake for n=2]
|
Linear signed ordering polytopes Q [science direct] (S. Fiorini, P. Fishburn)
convex_hull({char_vector_SLO | SLO a signed linear order with 2n elements})
|
Dimensions:
0, 1, 4, 9, 16, ... n^2
Number of Vertices in nth polytope:
1, 2, 8, 48, 384 ... 2^n*n!=(2n)!! [ OEIS A000165][see: i]
Number of Facets:
0, 2, 16, 82, 8480, ... OPEN [ OEIS ?]
f-vectors:
1, 2, 1, 8, 24, 32, 16, 1 ... [ OEIS ?]
|
Huffman Polytope, Huffmanhedron
[polymake for n=4]
|
Huffmanhedra, Huffman polytopes HP(n) [ResearchGate] (J. Maurras, T. Nguyen, V. Nguyen)DOI: 10.1016/j.dam.2012.05.004)
convex_hull({char_vector_t | t a Huffman tree with n leaves})
|
Dimensions:
0, 2, 4, 5, 6, ... n
Number of Vertices in nth polytope:
1, 1, 3, 13, 75, ... OPEN [ OEIS ?]
Number of Facets:
0, 3, 9, ... OPEN [ OEIS ?]
f-vectors:
1, 3, 3, 1, 13, 30, 26, 9, 1, ... [ OEIS ?]
|
Perfect Matching polytope of complete graph
(No 3d term.)
[polymake for 2n=6]
|
Perfect Matching polytope of complete graph on 2n nodes PM(n) = PM(K_2n) [wiki]
convex_hull({incidence_vector_PM | PM a perfect matching of the complete graph on 2n nodes}) [PNAS](P.Diaconis, S. Holmes)
Dimensions:
0, 2, 9, ...
Number of Vertices in nth polytope:
1, 3, 15, 105, ... (2n-1)!! [ OEIS A001147][see: i]
Number of Facets:
0, 3, 25, ... OPEN [ OEIS ?]
f-vectors:
1, 3, 3, 1, 15, 105, 435, 1095, 1657, 1470, 735, 195, 25, 1, ... [ OEIS ?]
|
|
Interval order polytope

(No 3d term.)
|
Interval order polytopes P_IO [citeseer] (R. Muller, A. Schulz) [wiki]
Interval order polytopes P_IO(D_n) of the complete digraph.
convex_hull({char_vector_IO | IO an interval order with n elements})
Dimensions:
0, 2, 6, ...
Number of Vertices in nth polytope:
1, 3, 19, 207, 3451, ... [ OEIS ]
Number of Facets:
0, 3, 17, ... OPEN [ OEIS ?]
f-vectors:
1, 3, 3, 1, 19, 96, 193, 183, 84, 17, 1, 207, ... [ OEIS ?]
|
|
Partial order polytope

(No 3d term.)
|
Partial order polytopes P_PO [science direct] (S. Fiorini)
convex_hull({char_vector_PO | PO a partial order with n elements})
Dimensions:
0, 2, 6, 12, ... n(n-1)
Number of Vertices in nth polytope:
1, 3, 19, 219, ... OPEN [ OEIS ?]
Number of Facets:
0, 3, 17, 128 ... OPEN [ OEIS ?]
f-vectors:
1, 3, 3, 1, 19, 96, 193, 183, 84, 17, 1, 219, 5791 ... [ OEIS ?]
|
|
Symmetric Traveling salesman polytope

(No 3d term.)
|
Symmetric Traveling Salesman polytopes STSP [zib.de]
(M. Grötschel, M. Padberg), [SMAPO library]
convex_hull({char_vector_HC | HC a Hamiltonian cycle of the complete graph on n nodes})
|
Dimensions:
0, 2, 5, 9, 14 ... n(n-3)/2
Number of Vertices in nth polytope:
1, 3, 12, 60, ... (n-1)!/2[ OEIS A001710]
Number of Facets:
0, 3, 20 ,100, 3437, 194187, 42104442,... OPEN [ OEIS ?]
f-vectors:
1, 3, 3, 1, 12, 60, 120, 90, 20, 1
... [ OEIS ?]
|
Asymmetric Traveling Salesman polytope
|
(No 2d,3d,4d terms.)
|
Asymmetric Traveling salesman polytopes ATSP(n)
[cornell] (L. Billera, A. Sarangarajan)
[science direct] (R. Euler,H. Le Verge)
convex_hull({char_vector_HC | HC a Hamiltonian cycle of the complete digraph on n nodes})
|
Dimensions:
1, 5, 11, 19 ... n(n-3)+1; n>2
Number of Vertices in polytope for n nodes:
2, 6, 24, 120, ... (n-1)![ OEIS A000142][see: i, ii, iii]
Number of Facets:
2, 6, 390, 319015,... OPEN [ OEIS ?]
f-vectors:
1, 2, 1, 6, 15, 20, 15, 6, 1, 24, ... [ OEIS ?]
|
Splitohedron

(No 3d term.)
[polymake for n=5,6]
[MatLab code for running PolySplit]
[also need matrix generator]
[and branch and bound algorithm]
[and distance algorithm]
[and RF-metric algorithm]
|
Splitohedra Sp_n [arxiv] (S. Forcey, L. Keefe, W. Sands)
relaxation of the Balanced Minimum Evolution Polytope BME(n).
intersection of half-spaces{split-facets, intersecting cherry facets,
caterpillar facets and the cherry clade-faces} from BME(n)
and also obeying the
{Kraft equalities}.
Dimensions (start n =3):
0, 2, 5, 9, 14 ... (n choose 2)-n
Number of Vertices in nth polytope:
1, 3, 27, 2335, ... OPEN [ OEIS ?]
Number of Facets:
0, 3, 40, 85, 161 ... (2^n+n^3-3n^2-2)/2 [ OEIS ?]
f-vectors:
1, 3, 3, 1, 27, 165, 310, 210, 40, 1, 2335, ... [ OEIS ?]
|
|
Balanced Minimum Evolution Polytope

(No 3d term.)
[polymake for n=5,6]
[faces and facets](2 page pdf.)
|
BME polytopes P_n = BME(n)
[arxiv]
(D. Haws, T. Hodge, R. Yoshida)
[almob]
(Eickmeyer et. al.)
[blog resources]
Balanced Minimal Evolution polytopes [arxiv], [arxiv](Forcey et. al.)
convex_hull({dist_vector_T | T a binary tree with n labeled leaves})
Dimensions (start n =3):
0, 2, 5, 9, 14 ... (n choose 2)-n
Number of Vertices in nth polytope:
1, 3, 15, 105, ... (2n-5)!! [ OEIS A001147][see: i]
Number of Facets:
0, 3, 52, 90262... OPEN [ OEIS ?]
f-vectors:
1, 3, 3, 1, 15, 105, 250, 210, 52, 1, 105, 5460... [ OEIS ?]
|
|
Acyclic subgraph polytope

(No 3d term.)
[polymake for n=3]
|
Acyclic subgraph polytopes P_AC [ULB] (S. Fiorini)
[springer] (M. Grötschel, M. Jünger, G. Reinelt),
[MIT] (M. Goemans, L. Hall)
convex_hull({char_vector_AC | AC an acyclic subgraph of complete digraph on n nodes})
Dicycle covering polytope P_DC [ULB] (S. Fiorini)
convex_hull({<1,...,1> - char_vector_AC | AC an acyclic subgraph of complete digraph on n nodes})
|
Dimensions:
0, 2, 6, 12, ... n(n-1)
Number of Vertices in nth polytope:
1, 3, 25, 543, 29281, ... [ OEIS A003024]
Number of Facets:
0, 3, 11 ... OPEN [ OEIS ?]
f-vectors:
1, 3, 3, 1, 25, 93, 142, 111, 48, 11, 1, ... [ OEIS ?]
|
Weak order polytope

(No 3d term.)
|
Weak order polytopes P_WO [science direct] (S. Fiorini, P. Fishburn)
convex_hull({char_vector_WO | WO a weak order with n elements})
Dimensions:
0, 2, 6, 12, ... n(n-1)
Number of Vertices in nth polytope:
1, 3, 13, 75, ... sum{k=0..inf} (k^n)/(2^(k-1))[ OEIS A000670]
Number of Facets:
0, 3, 15, 106 ... OPEN [ OEIS ?]
f-vectors:
1, 3, 3, 1, 13, ... [ OEIS ?]
|
|
coming: Graphical Traveling salesman polytope GTSP(n) [SMAPO library]
** 3d term is simple but probably not later terms.
ARRAYS (two or more indices) (we are trying to decide how to organize these!)
Full entry coming soon:
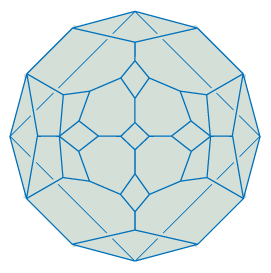
(0, 22, 0, 0, 8)
|
Cyclic polytopes C(n,m) ...
[ wiki]
Pairahedra Ph(n,m) ... (0, 4, 4, 3) I(2,1)= I(1,2) [T. Tradler],[ T. Tradler]
Finite product lattice polytopes P_(l,m,...,k) ... (0, 4, 4, 3) P_(1,2)
[J. Bloom]
Resultohedra (indexed by trees) ... (0,4,4,4); (0, 7, 6, 6) [M. Batanin, via R. Street] [arxiv](Batanin)
(Step 2) Biassociahedra KK(n,m) = B^n_m ... KK(2,3) = KK(3,2)= heptagon [arxiv](M. Markl)
[arxiv](S.Saneblidze, R. Umble)
... KK(2,4) = KK(4,2) =
(0, 13, 3, 0, 5), 32 vert. 21 facets
[arxiv](M. Markl)
KK(3,3) =
(0, 22, 0, 0, 8), 44 vert. 30 facets
[arxiv](M. Markl)
Bimultiplihedra JJ(n,m)
... JJ(2,2) = octagon ; JJ(2,3) =(0, 19, 0, 3, 4, 0, 0, 2) 46 vert. 28 facets [arxiv] (S.Saneblidze, R. Umble)
(Step 2) Bipermutahedra PP(n,m)
... PP(1,2) = heptagon; PP(2,2) = KK(3,3) =
(0, 22, 0, 0, 8), 44 vert. 30 facets; [arxiv](S.Saneblidze, R. Umble)
Operahedra G. Laplante-Anfossi
Shuffles of deformed polytopes F. Chapoton, Pilaud
Higher Secondary polytopes. Galashin, Postnikov, Williams
Galashin's Poset associahedra P. Galashin
Bridge polytopes L. Williams
Constrainahedra N. Bottman, D. Poliakova
Ordered partial partition polytopes R. Houston, A. P. Goucher, N. Johnston
Cosmohedra Nima Arkani-Hamed, Carolina Figueiredo, Francisco Vazão
Graph Cosmohedra Ross Glew, Tomasz Lukowski
Correlator polytopes Carolina Figueiredo, Francisco Vazão
Acyclonestohedra
Chiara Mantovani, Arnau Padrol, and Vincent Pilaud
Acyclonesto-Cosmohedra
Stefan Forcey, Ross Glew, Hyungrok Kim
Fibonacci polytopes, FP_n(k).
Fred J. Rispoli
Kostka polytopes Amanda Burcroff
Hypergraphic polytopes
Carolina Benedetti, Nantel Bergeron, John Machacek
Binomial polytopes
Silvio Ursic
Oriented Matroid Circuit Polytopes Laura Escobar, Jodi McWhirter
Symmetric edge polytopes Tianran Chen, Robert Davis, Evgeniia Korchevskaia
Truncated trapezohedron wiki
|
|
INDEX
2-associahedra
- Acyclic subgraph polytope
Acyclonestohedra
Acyclonesto-cosmohedra
- Acyclotopes: see Graphical Zonotopes
- Acyclotope (cycle graph)
- Alternating Sign Matrix Polytope
- Amplituhedron for biadjoint scalar phi^3 theory
- Asymmetric Traveling Salesman polytope
- Associahedron
Amplituhedra
- Balanced Minimum Evolution Polytope
- Beam Polytope
- Biassociahedra
- Bimultiplihedra
Binomial polytopes
- Bipartite Subgraph polytope
- Birkhoff polytope
Brick Polytopes
- Bridge polytopes
- Cayley Polytopes
- Chan-Robbins-Yuen Polytopes CRY(n-1)
Chain Polytopes
- Composihedron
Constrainahedra
- Correlation polytope
- Cosmohedron
Coxeter Associahedra and Permutahedra
- Cube
- Cubeahedron(edgeless graph)
- Cut Polytope
- Cycle Graph multiplihedron
Cyclic polytopes
- Cyclohedron
- Demihypercube
- Diagonal rectangulation polytope
- Dürer's solid
- Edgeless-graph-associahedra
Fiber polytopes
Fibonacci polytopes
- Finite product lattice polytopes
- Flow polytopes
- Freehedron
Graph Associahedra
Graph Composihedra
Graph Cosmohedra
Graph Cubeahedra
Graph Multiplihedra
- Graphical Traveling Salesman polytope
Graphical Zonotopes
- Graph composihedron (cycle graph)
- Graph composihedron (edgeless graph)
- Graph multiplihedron (cycle graph)
- Graph multiplihedron (edgeless graph)
- Halohedron
- Higher Secondary polytopes
- Huffman Polytope
- Hypercube
- Hypergraphic polytopes
- Independent set polytope of Uniform matroid
- Interval order polytope
- Linear Ordering Polytope
- Linear signed order polytope
Matching Polytopes
Multiassociahedra ((k-crossing)-free diagonalizations of n-gon)
Multiplihedra
Operahedra
- Ordered partial partition polytopes
Order Polytopes
- Pairahedra
- Partial order polytope
- Path-graph Tubing polytope
- Path polytope
- Perfect Matching Polytopes: see Matching Polytopes
- Permutohedron/ permutahedron
- Permutoassociahedron
Poset Associahedra
- Pterahedron
Quotientopes
- Quotientope: Basic shards
- Quotientope: Complete set of shards
- Quotientope: Upper shards
- Quotientope: Upper shards and lower shards
- Quotientope: shards (1, 3, {2}), and (1, 3, {})
- Quotientope: shards (i, i+2, {i+1}), and (i, i+2, {})
Rectangulotopes
- Resultohedra
- Simplex
Secondary Polytopes
Shuffle Polytopes
- Splitohedron
- Stanley-Pitman Polytope
- Stellohedron
- Symmetric Traveling Salesman polytope
Traveling Salesman Polytopes
- Tribonacci polytopes
- Truncated trapezohedra
Tubing Polytopes
- Tutte Polytope
- Type A Coxeter-associahedron (Permutoassociahedron)
- Type B Coxeter-associahedron
- Type B permutohedron
- Type D Associahedron
- Type D Coxeter-associahedra
- Type D permutohedron
- Vertex cover polytope: complete graph
- Weak order polytope
- Zonotopes: see Graphical Zonotopes
Conjectured
simplicial complex of k-triangulations or k-tubings .
Species compositions: Painted tree polytopes .
pseudograph-multiplihedra, poset multiplihedra.
Back to research page.
Revision Year: 2025





























































