Back to big table.
Acyclotope (cycle graph)
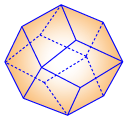 (0, 12, 0, 0) |
• Acyclotopes for cycle graph A(G) [ Zaslavsky] • Graphical zonotopes for cycle graph Z(G) [Postnikov] • Voronoi cells of cographical lattice for cycle graphs (primary parallelohedra, primary parallelotopes) [F. Vallentin] • Brillouin zone (Wigner-Seitz cell of reciprocal space) for Body Centered Cubic lattice in 3d [wiki] |
• Dimensions: 0, 1, 2, 3, ... n • Number of Vertices in nth polytope: 1, 2, 6, 14, 30, ... acyclic orientations of (n+1)-cycle = 2^(n+1) - 2 [ OEIS A000918] • Number of Facets: 0, 2, 6, 12, 20, ... directed edge cuts of the (n+1)-cycle = n^2+n [ OEIS A002378] |
top index
The 3d case is the rhombic dodecahedron.