...but it is growing. Send entry suggestions to: Entry Editor
Searching the table:
- Ctrl-F, keywords.
- or use the index of named problems.
Topical Map to all the problems.
Each entry of this list is an open problem, but it might have been solved by the time you see it!
Google lots before assuming otherwise.
Links are to introductory literature, not necessarily primary sources.
PROBLEMS
Number of affine plane arrangements in 3D
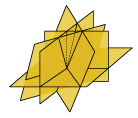 |
|
1, 1, 2, 5, 14, 74, 1854, 1472049 ... OPEN |
top index
Kobon triangles
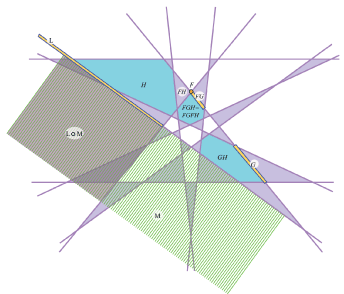 |
|
1, 2, 5, 7, 11, 15, 21, ... OPEN [ OEIS ?] |
top index
Ribbon-Slice conjecture
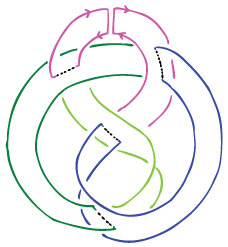 |
|
|
top index
Snake in a Box
 |
|
1, 2, 4, 7, 13, 26, 50, 98, ... OPEN [ OEIS ] |
top index
Moore bounds
 |
|
1, 1, 4, 3, 13, 21, ... OPEN [ OEIS ] |
top index
Affine line arrangments
 |
|
1, 1, 2, 4, 9, 47, 791, 37830, ... OPEN [ OEIS ] |
top index
Number of posets
 |
|
1, 1, 2, 5, 16, 63, 318, 2045, ... OPEN [ OEIS ] |
top index
Ramsey numbers.
 |
or k of them are mutual strangers? such that there is either a red or a blue complete subgraph of size k? |
0, 1, 2, 6, 18, 45, 102, 213, 426, 821, ... [ OEIS ] |
top index
Snaky: winner or loser
 |
or can it be blocked by player 2? |
|
top index
Singmaster's conjecture
 |
|
2, 3, 6, 10, 120, 120, 3003, 3003, ... OPEN [ OEIS ] |
top index
Invertible (0,1)-Matrices
 |
|
1, 1, 6, 174, 22560, 12514320, ... OPEN [ OEIS ] |
top index
Hadamard's maximal determinant problem
 |
|
1, 1, 2, 3, 5, 9, 32, 56, 144, 320, ... OPEN [ OEIS ] |
top index
- Are there more than 5 Fermat primes? (more than 31 constructible odd-sided regular polygons?)
- Is every even number >0 the sum of two primes?
- Is there an infinite number of Mersenne primes?
- Is there an infinite number of twin primes?
- Does the Collatz sequence always end in 1?
- Does every finite connected vertex-transitive graph contain a Hamiltonian cycle except the five known counterexamples?
- Is Catalan's constant irrational?
- How many finite topologies are there, with n elements?
- How many graphs are there up to isomorphism on n nodes?
- How many transitive relations are there on a set with n elements?
- How many distinct combinatorial polytopes are there, in 3D, with n vertices?
- Do two knots with n, m respective minimum crossings connect-sum to a knot with n+m crossing number?
- Do two knots with n, m respective unknotting numbers connect-sum to a knot with at least n+m-1 unknotting number?
- Can the triple connected sum of some knot (3 copies) be cobordant to the unknot? slice? ribbon?
- Is every self-inverse-concordant knot (having 2-torsion) amphichiral?
- Are the nontrivial zeroes of the Riemann zeta function all on the line Re(z) =1/2?
- Is the diameter of a polytope always found by a polynomial using its number of facets and dimension? (Polynomial Hersch)
- What are the homotopy groups of spheres? Stable homotopy groups of spheres? The ways to map a 70-dimensional sphere onto a 2-sphere?
- What is the value of the busy beaver function for n=6? That is, what is the maximal number of steps that an n-state, 2-symbol, d+ in {LEFT, RIGHT}, 5-tuple (q, s, q+, s+, d+) Turing machine can make on an initially blank tape and then halt?
- Can a thrackle have more edges than vertices?
- Does every convex polyhedron have a net?
- How many nets does the n-dimensional hypercube have?
- Is the Mandlebrot set path-connected?
- Are multiassociahedra polytopes? (Does Loday's realization generalize?)
- Are pseudograph-multiplihedra polytopes? Poset multiplihedra?
- Does P = NP? Is there a polynomial time method to decide if a logical expression is a contradiction or not?
- Is pi + e irrational?
- Does every finite sequence of numbers appear in pi?
- Is pi normal? e?
- Is the (computable) omega constant normal? (This omega is the solution to xe^x=1.)
- What is the sixth bit of the incomputable (normal) Omega corresponding to the Busy Beaver problem? (This omega is Chaitin's constant.)
- What is the input n for the busy beaver value that would determine Goldbach?
- Is there a finite projective plane of order 12?
- How many unique (up to constant factor) non-negative solutions to n-1 homogeneous linearly independent linear equations in n variables using 1, 0 ,-1 as coefficients are there?
- How many oriented matroids are there on a base set of size n? Up to isomorphism?
- How many incidence geometries are there for n points? n lines? Up to isomorphism?
INDEX
| # | | A | | B | | C | | D | | E | | F | | G | | H | | I | | J | | K | | L | | M | | N | | O | | P | | Q | | R | | S | | T | | U | | V | | X | | Y | | Z | |
Determinants of Invertible (0,1)-Matrices
Hadamard's maximal determinant problem
Kobon triangles
Line arrangments (affine)
Moore graphs
Plane arrangements in 3D, affine
Poset counting
Ramsey problem
Ribbon-Slice conjecture
Singmaster's conjecture
Snaky achievement
Snake in a Box
top index
Back to research page.
Revision Date: