Towards a theory of derived braids and their categories.
I. Braid relation, ribbons, and the opposite of an enriched category.
II. Products of enriched categories and derived braids.
III. Questions and conjectures.
We begin by describing a geometrical reformulation of the braid relation.
The first slide shows this process.
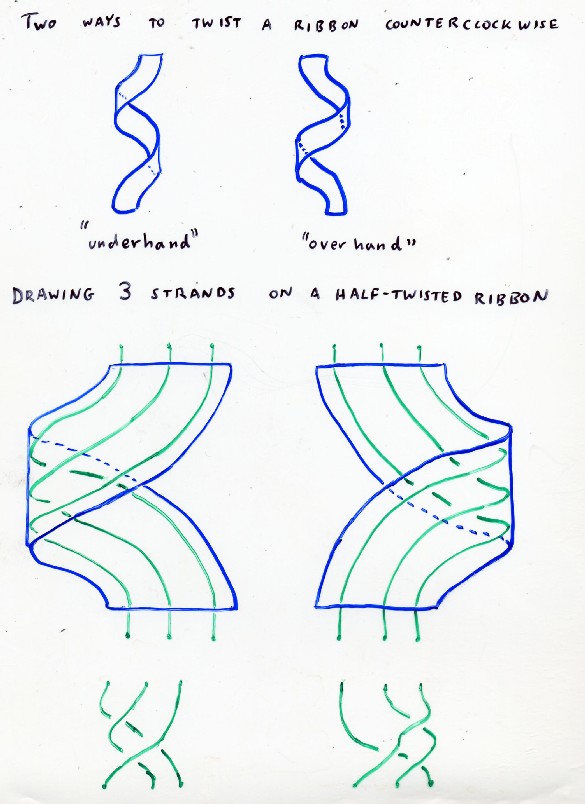
So the Yang-Baxter braid relation can be seen as the equivalence of under and overhanded twists. Next we
generalize.

Now switch gears and think about categories: first the basic definitions.

We can't neglect to relate the Y-B equation to naturality.

Now for a further level of definitions: enriched categories.

There are structures defined on V-Cat if there is structure on V.
First we define the opposite of a V-category if V is braided, and
show that it is a valid V-category. Recall that Joyal and Street proved
coherence for braided categories: if two legs of a diagram made up of
the canonical natural transformations have the same underlying braid
then the two legs are equal--the diagram commutes.
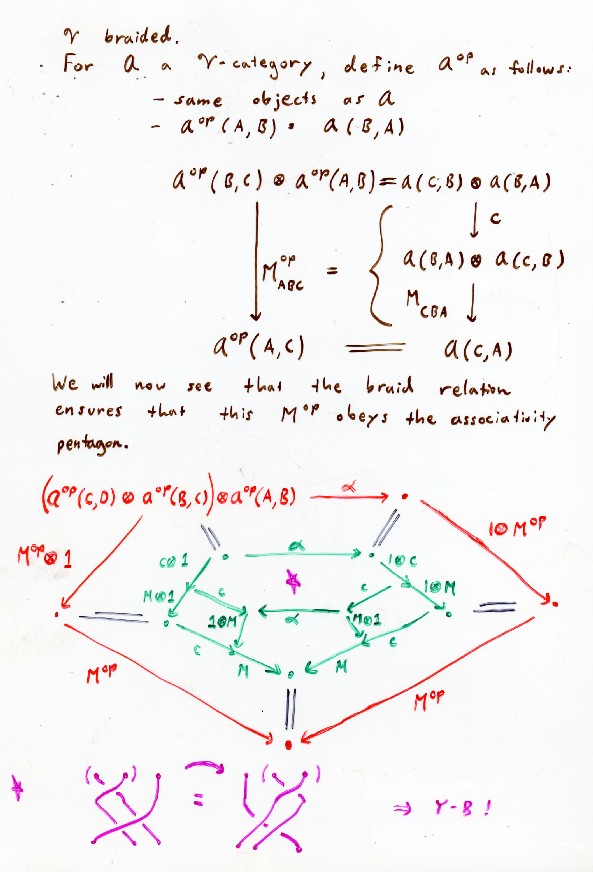

We note that there is a reverse sort of op called "co" that is completely analogous but that uses c^-1.
Now another important structure: product on V-Cat.


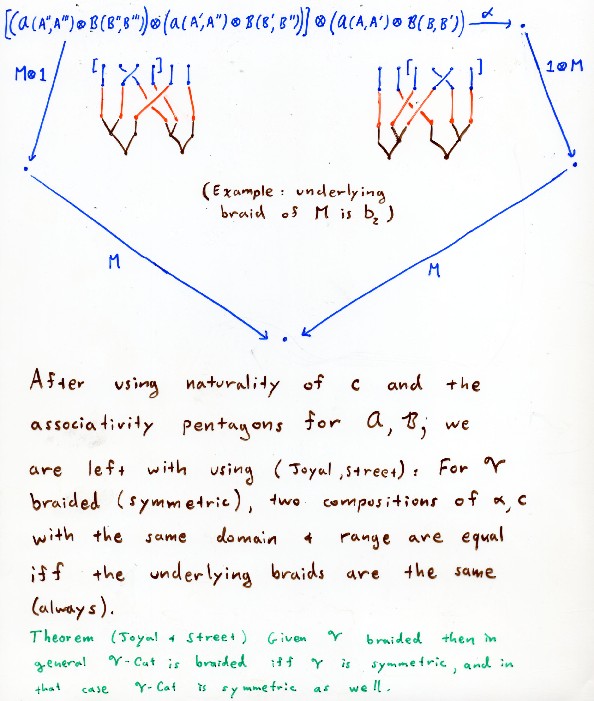
We note that there is another product, tensor', that uses c^-1.
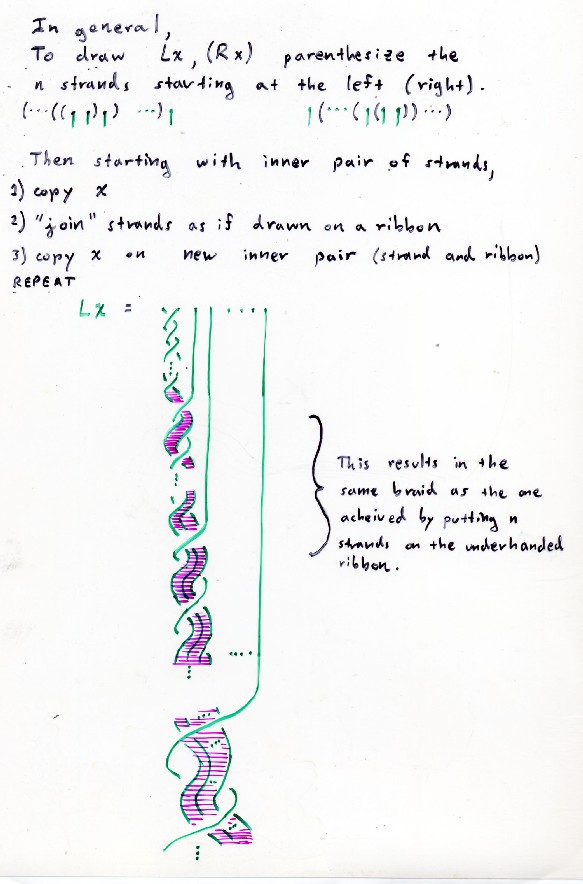
We can now generate lots of braid equalities by combining
the two structures of opposite and product enriched categories. For instance, the next slide
shows the left and right derived braids underlying the two legs of the pentagon when
the enriched category involved is A^opop tensor B^opop. It also includes the instructions
for forming Lx and Rx in B_6 for x in B_4 .
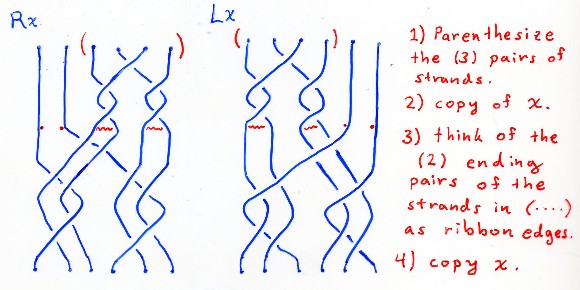
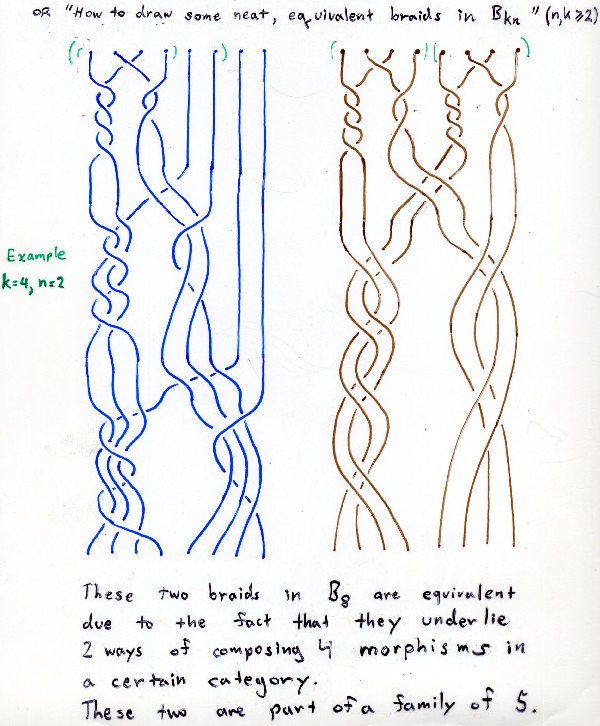
The next family of braids come from composing 4 hom-objects in the product of 2 enriched categories: A^cocococo tensor B^opop.
The lesson to be learned is that if the braid x in B_2n has Lx=Rx in B_3n then the categorical interpretation implies
that if x underlies a composition morphism then it has Lx=Rx in B_kn for all k>2 in N.

In fact we can describe
sufficient conditions for Lb to be equivalent to Rb by describing the braids b that underlie
the composition morphism of a product category given generally by
((({\cal A}^{op})^{...op}\otimes^{(1)} ({\cal B}^{op})^{...op})^{op})^{...op} where the number of
op exponents is arbitrary in each position. Those braids are alternately described as lying in
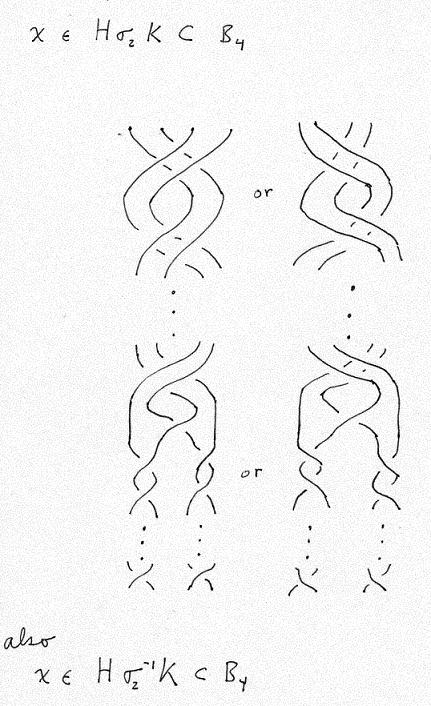
H\sigma_2K \subset B_4 where H is the cyclic subgroup generated by the braid \sigma_2\sigma_1\sigma_3\sigma_2
and K is the subgroup generated by the two generators {\sigma_1, \sigma_3}. We use \sigma for the classical braid group generators.
The latter subgroup K is isomorphic to Z\times Z. The first coordinate corresponds to the number of
op exponents on A and the second component to the number of op exponents on B (when positive-to co when negative). The
positive power of the element of H corresponds to the
number of op exponents on the product of the two enriched categories, that is, the number of
op exponents outside the parentheses. That b is in H\sigma_2K implies Lb=Rb follows from the
fact that the composition morphisms belonging to the opposite of a V-category obey the
pentagon axiom. An exercise of some value is to check consistency of the definitions by constructing
an inductive proof of the implication based on braid group generators.
This is not a necessary condition.
Here is a picture of x in B_4 such that Lx=Rx.
When the number n of enriched categories in a product category increases, the number
of braids in B_(2n) such that Lx=Rx in B_(3n) grows quickly, using op, co, various parenthizations, and both
tensor and tensor' to combine the enriched categories.
Questions include: Which of these braids can be used in place of \sigma_2 in order to define an associative
product on V-Cat? My conjecture is none of them (see section 3 of "Enrichment as categorical delooping I.")
Are there any braids in B_2n with Lx=Rx but that do not either underlie a product of enriched categories or
do so after joining some adjacent strands which always remain adjacent? How do we construct and interpret the odd n analogues of all
this?
Another conjecture: In B_2n consider the following braids:
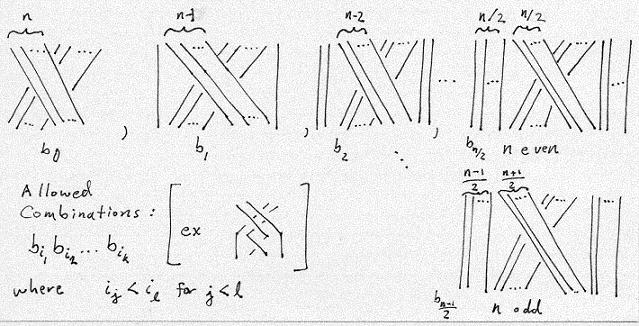
We conjecture that the allowed combinations ("decreasing products") obey Lx=Rx.
Back to research page.
















